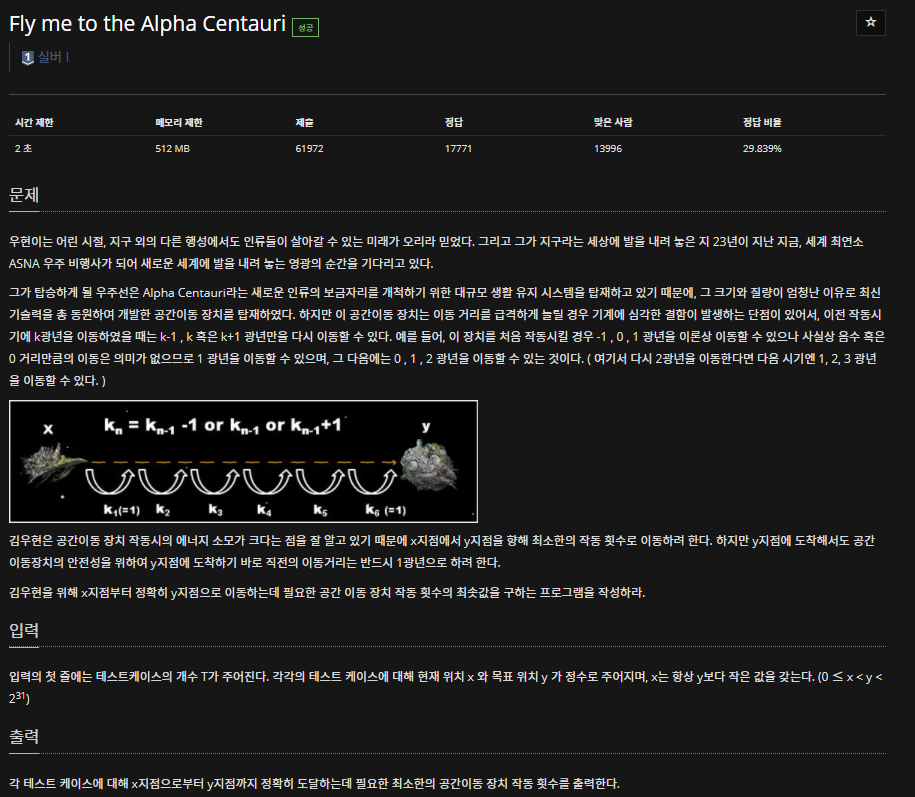
안녕하세요 오늘은 특정한 알고리즘을 사용하는 것이 아닌 수학적 사고력을 이용한 문제를 풀어보겠습니다. 이 문제는 특정한 알고리즘을 생각해내는것보다 단순히 이 문제의 원리를 생각해야합니다. 코드: #include #include using namespace std; int main(){ ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); int t; cin>>t; for(int i = 0; i>x>>y; if(y-x == 1){ cout